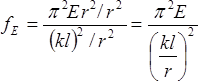| Home | Module 1 | Module 2 | Tutorials | Credits | Contact Us |
<<Back to the Previous Page <<Fundamentals <<Knowledgebase Fundamentals |
Buckling of Compression Members Euler Buckling Load When a structural member is subjected to compressive stresses at certain levels, it deflects outward (similar to bending). This is called “buckling”. The load at which a compression member buckles is called the “critical load” (Pcr) or the Euler Buckling Load (PE) after Leonhard Euler, the Swiss mathematician, who computed it about three hundred years ago:
In this equation, π = 3.14, E is the modulus of elasticity (psi or ksi), Ι is the moment of inertia (in4) about which the column buckles, kl is the effective length of the column against buckling (ft or in.), and PE (or Pcr) is the Euler Buckling Load (in lb or kips).
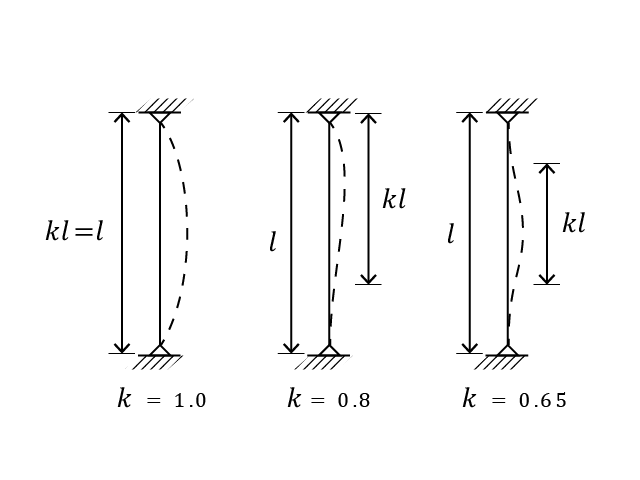
The column effective length depends on its length, l, and the effective length factor, k. k depends on the type of columns’ end conditions. If the member is pin-ended (it can freely rotate), k=1.0. This means that the entire length of the member is effective in buckling as it bends in one-direction. If one or both ends of a column are fixed, the effective length factor is less than 1.0 as shown below. This means that the member buckles at a larger load or it is more difficult to make it buckle.
Euler Buckling Stress To compute the Euler buckling stress, fE, we divide the Euler buckling load, PE, by the member’s cross-sectional area, A:
Substitute
Dividing the numerator and denominator by r2:
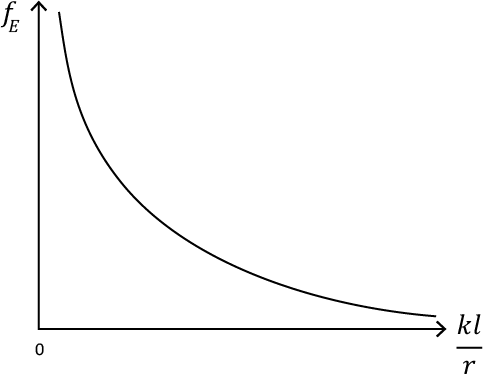
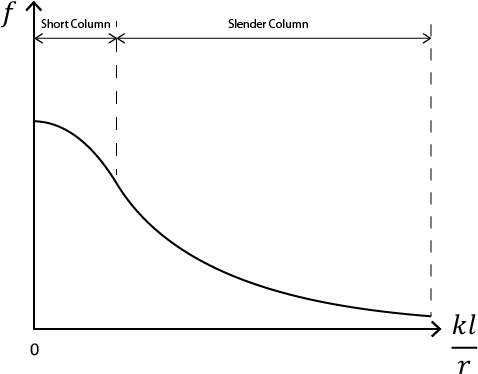
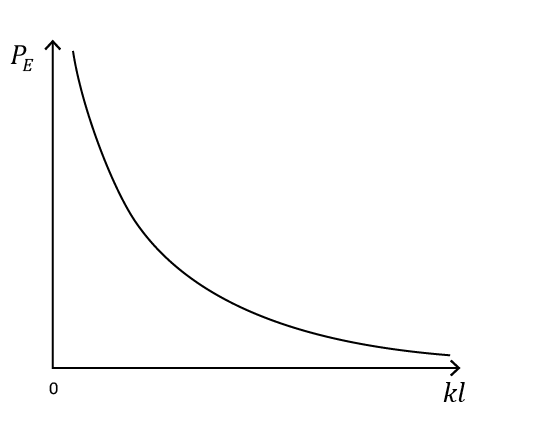
The variation of fE versus
It is clear that for very small
|
© 2011 Virginia Polytechnic Institute and State University
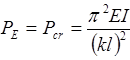
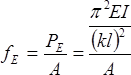
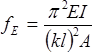
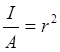 (r is defined as
(r is defined as