| Home | Module 1 | Module 2 | Tutorials | Credits | Contact Us |
<<Back to the Previous Page <<Fundamentals <<Knowledgebase Fundamentals |
||
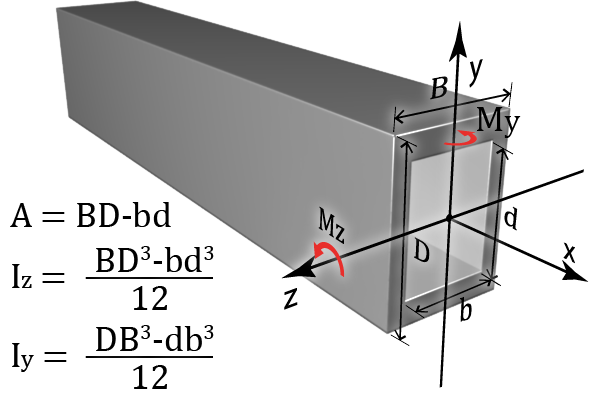
Geometric Properties of Areas There are several geometric properties of the cross-section of a structural member which are important in terms of the member's behavior under loads:
Area or Cross Sectional Area (A): This is the area of the section when cut perpendicular to the longitudinal (or x-) axis. It is easy to compute this property which also has an explicit physical meaning.
In terms of the behavior of a structural member, A, represents the axial and shear stiffness.
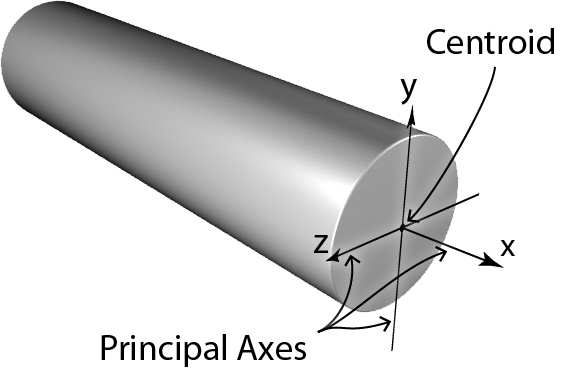
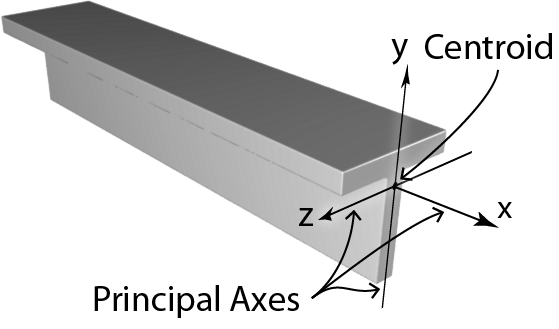
Principal Axes and Centroid: The principal axes are the main axes of a member which are perpendicular and intersect each other at the center of area or “centroid”. One can think of the centroid as the center of gravity of an object if it is made of one material (homogeneous).
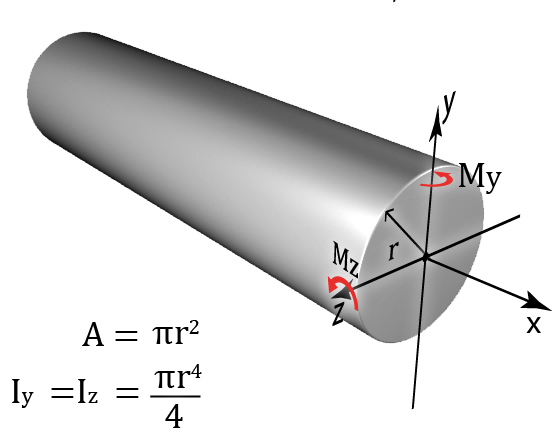
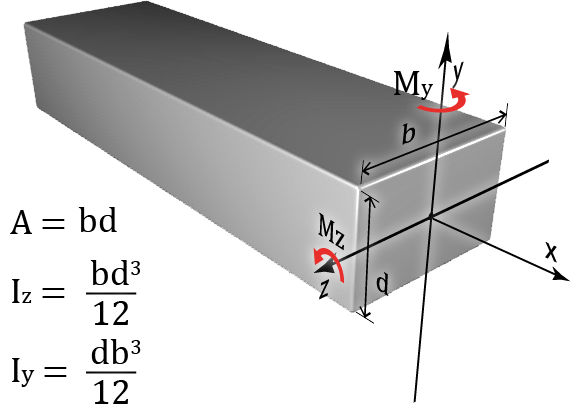
Moment of Inertia (I): Moment of inertia does not have an explicit physical meaning, i.e., one cannot observe it. However, it represents the bending stiffness of the structural member, i.e., how difficult it is to bend it. A higher value for a member's moment of inertia translates to a stiffer member. Since there are two bending axes in a two-dimensional space(y and z), we have two values of moment of inertia defined about each axis. It is usually measured in units of (in4).
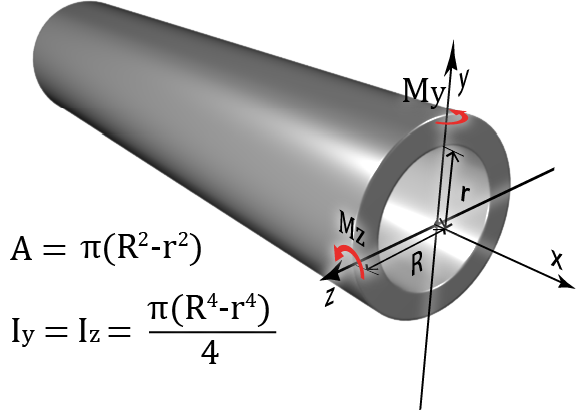
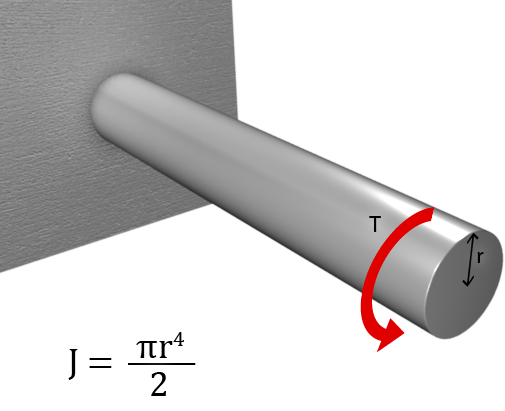
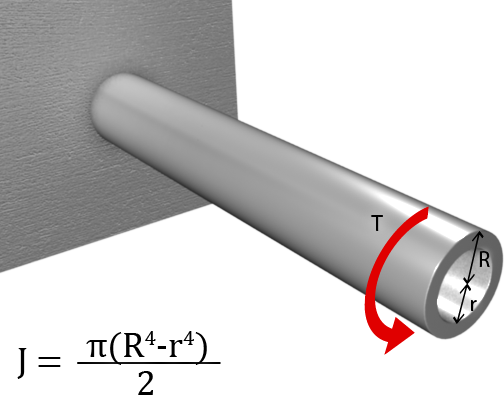
In addition to the moments of inertia about the two main axes, we have polar moment of inertia, J, which represents the stiffness of circular members such as solid shafts and hollow structural sections against torsion.
Torsion of a Solid Shaft
Torsion of a Hollow Structural Section Torsion of a hollow structural section
Radius of Gyration (r): Similar to the moment of inertia, radius of gyration does not have an explicit physical meaning. The radius of gyration is defined as:
|
© 2011 Virginia Polytechnic Institute and State University
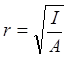 or
or