Tensile, Compressive and Bending Stresses and Strains

Stress represents the action of a force or moment on a structural member. If the force pulls the member (tension) it results in a tensile stress; if the force pushes the member (compression) it results in compressive stress. Tensile stresses stretch a member and compressive stresses squeeze a member.

There is a significant difference between the behavior of a structural member in tension and compression. Depending on how slender the structural member is, it may buckle or crush under compression stresses. However, buckling does not occur when a structural member is subjected to tensile stresses. Stress (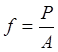) is defined as force () divided by area ():

  

has units of  lb/in² (psi) or k/in² (ksi)

Compression Stress Distribution

Tensile stress results in the elongation of the member. If the original length is (l) and the change in the length is , strain () is defined as:  
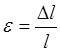Therefore, stress represents the applied force and strain represents the resulting deformation.

Tensile Stress Distribution

Bending is due to the internal moment. Since moment can be resolved into a couple, the internal moment can be considered as a compression force (C) and a tensile force (T). The compression force results in compressive stresses and tensile force in tensile stresses. Therefore, bending stress is a combination of compressive and tensile stresses due to  internal moments.

Since the stress across a beam section varies from compression to tension, there is a location at which stress is equal to zero. This is called the “neutral axis”. For a homogeneous beam the neutral axis passes through its centroid.

Bending Stress Distribution

<<Back to the Previous Page <<Fundamentals <<Knowledgebase